
By John SanGiovanni (@JohnSanGiovanni), coauthor of the Mastering the Basic Math Facts series
Stop me if you’ve heard this one before. Three students walk into a math classroom. They confront 709 – 340. Krista uses a number line to count back with three jumps of 100, a jump of 50, and another jump of 19. She then adds her jumps. Damian solves with paper and pencil. Oscar counts up mentally from 340 to 640 (300) and then 640 to 709 (69 more) to compose a difference of 369. So which student selected and used tools strategically?
The answer depends on our interpretation of tools, our expectations for using tools, and the mathematical maturity of our students. So what constitutes a tool? (Insert joke here!) Clearly, protractors, rulers, graphing calculators, and manipulatives like color tiles qualify. Paper and pencils do, too. Simply, a tool is anything that aids in accomplishing a task (including Krista’s number line).
 What is unique about Practice #5 is the idea that these tools are used strategically. In many situations, paper and pencil are inefficient and using them is not strategic. We must develop the notion that mental computations are possible, reliable, and often more efficient. Oscar shows mental computation at its finest. Consider Krista and Damian. Which pathway is strategic? It depends if they are a third grader, a fifth grader, or a ninth grader.
What is unique about Practice #5 is the idea that these tools are used strategically. In many situations, paper and pencil are inefficient and using them is not strategic. We must develop the notion that mental computations are possible, reliable, and often more efficient. Oscar shows mental computation at its finest. Consider Krista and Damian. Which pathway is strategic? It depends if they are a third grader, a fifth grader, or a ninth grader.
Using a calculator should also be a strategic decision. It should be a tool that provides access, simplifies the task, or confirms accuracy. It doesn’t make sense for a fifth grader to use a calculator for 8 + 13. However, it may make perfect sense for a first grader to confirm the sum that way. Consider 8.1258 + 12.14920. Is this a mental math activity? Does it call for paper and pencil? Does it make sense to use a calculator? Better yet, do our students have opportunities to discuss when they might use either of these tools? Do our students have the freedom to use or not to use these tools as they deem necessary?
We must also recognize that tools do not produce understanding, problem solving, and solutions. These come from the individual. I cannot assume that providing a student with a protractor ensures that they will find angle sums with accuracy. Similarly, a graphing calculator doesn’t consider user error or misconception when graphing a linear equation.
User error (including broken buttons) can occur when using basic calculators. Yet when something goes wrong, we pause. We consider. We adjust. We try the tool again. How does our thinking factor into using tools? What questions do we want our students to ask when selecting and using tools? To me, these key questions include:
- “Do I need a tool?”
- “What tool is the best to use?”
- “How does it work?”
- “Do the results align with what I was expecting?” or “Do the results make sense?”
Concepts must be developed with the tool, even reinforced by the tool. The use of the tool itself should support reasoning rather than mere procedure. In other words, students must understand angles prior to using a protractor but also reinforce this understanding while using the protractor. Using a protractor is more than “lining it up the right way.” Understanding enables them to be proficient in diverse situations and even with diverse protractors. Consider these four examples:
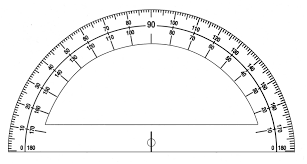 This protractor is dual sided and the base of the protactor aligns with the 0/180 line. This protractor is dual sided and the base of the protactor aligns with the 0/180 line.
|
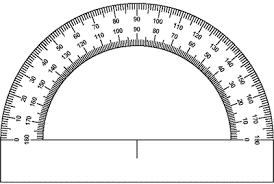 This protractor is dual sided but the base of the protractor is not aligned with the 0/180 line. This protractor is dual sided but the base of the protractor is not aligned with the 0/180 line.
|
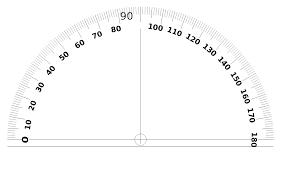 This protractor is not dual sided but the base aligns with the 0/180 degree line. This protractor is not dual sided but the base aligns with the 0/180 degree line.
|
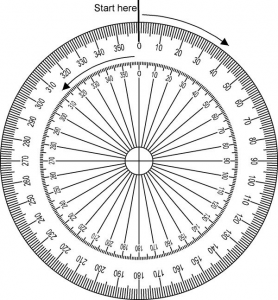 This protractor shows a full rotation of 360 degrees. This protractor shows a full rotation of 360 degrees.
|
They all measure angles but each does so in a different way. What understanding must a student have to use each of these effectively?
Understanding helps us realize accuracy. Consider 8.1258 + 12.14920 from above. If I use a calculator, I should know that my sum will be in the neighborhood of 20. I need to reconsider if my calculator result is dramatically different. The idea of understanding holds true for other tools including paper/pencil. It transcends grade level. For example, if I determine that my slope is negative and my line rises from left to right, then something is awry.
We play a critical role in the development of strategic use of tools. First, we make tools available to our students. We encourage their strategic use. We model using them. We don’t admonish students who choose to use them. Instead, we ask them to share their reasoning for using a tool. We identify how tools connect to the ideas of mathematics. We make varieties of tools available for a situation and provide variety in the tools themselves when possible (i.e. different protractors).
Most importantly, we constantly develop the metacognitive process of tool selection and use. This development is centered on the bulleted questions above. We lift up the thinking behind the tool as well as the procedure for using the tool. We require our students to either predict what their finding might be prior to using the tool. Or, we require a reflection on the results and if they make sense.
Tools are meant to make sense of mathematics and the world around us. They are meant to improve efficiency and support accuracy. They are a part of modern life—as is our responsibility to understand them, use them strategically, and develop these proficiencies in our students.
 |
 |
 John SanGiovanni is the coauthor of the best-selling books Mastering the Basic Math Facts in Addition and Subtraction and Mastering the Basic Math Facts in Multiplication and Division. He is also the coauthor of Putting the Practices Into Action, which examines the Standards for Mathematical Practice and unpacks their power for developing deep mathematical understanding in students. Follow him on Twitter @JohnSanGiovanni.
John SanGiovanni is the coauthor of the best-selling books Mastering the Basic Math Facts in Addition and Subtraction and Mastering the Basic Math Facts in Multiplication and Division. He is also the coauthor of Putting the Practices Into Action, which examines the Standards for Mathematical Practice and unpacks their power for developing deep mathematical understanding in students. Follow him on Twitter @JohnSanGiovanni.



