Last spring I went on sabbatical and did some practical learning research. It changed my teaching life in ways I’m still trying to grasp.
In my first blog I shared my growing sense that there must be a better way to teach math. I told you about workshops and readings that suggested visuals might be the path. In my second blog I shared one of many remarkable moments when my fifth-grade students showed me what they could do with visuals.
Having seen how visuals engaged my fifth graders, I built my sabbatical around experiments with visual tools in more than a dozen classrooms from first to ninth grade. I’m still making sense of the lessons students taught me about the ways visual supports led them to engaged, hands-on math inquiry. But I know I’ve changed because, suddenly, I have a renewed passion for teaching math.
So much so that last June I found myself applying for a job as a high school math teacher. Mind you, I have no secondary certification, no real experience with higher-level math, not to mention very little experience teaching older students. This was a sudden leap of faith inspired by my growing conviction that the way I saw young learners engage with visuals ought to work with older learners as well. Why not?
Looking back now, I see that my interview with the high school principal and my classroom demonstration that followed were a bit unusual.
Principal: Are you certified to teach high school math?
Me: No.
Principal: Can you teach all levels of math?
Me: Well . . . no. But I’m pretty sure I can teach algebra, and maybe geometry!
Principal: (blink, blink)
Me: (frozen smile)
That’s how I arrived, one week later, for a demonstration lesson in front of a group of ninth-grade honors math students (and with two high school math teachers and an assistant principal in the back of the classroom).
I opened my lesson . . .
“As always,” I said to everyone, “your job is to think like mathematicians. Today, while you build this pattern . . .” I pointed to the slide (Figure 1).
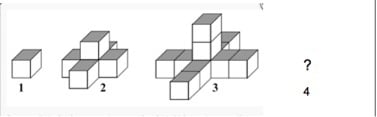Figure 1
“. . . Look for repetition in the ways you build and in the ways you count.”*
I knew this lesson might raise eyebrows in the back of the room, especially coming from a guy who refused to stay in his lane (elementary school). But I’d seen exciting results with younger students that strongly suggested the same engaged learning could be found with any level mathematician. Or, perhaps this really was a crazy leap of faith. Either way, I had to see for myself.
I handed out containers of centimeter cubes and asked the ninth graders to use them to build the next stage in the pattern (stage 4) and to figure out how many blocks they would need to build the tenth stage. (You, dear reader, may want to grab some blocks and try this before reading on. It’s fun!)
*This lesson is adapted from a lesson in Routines for Reasoning: Fostering the Mathematical Practices in All Students, a book published by Heinemann in 2016 and fully referenced below.
Before we’d really even begun, I was called out on my audacity.
“This is an honors class,” one of the ninth graders grumbled.
Chances are good this student was shooting me a reminder that, at their honors level, manipulatives were maybe a bit insulting.
I moved on without comment. To my relief, everyone else did too. The rest of the class popped open their containers and proceeded to build the pattern stages in the problem.
“Look and listen to repetition in your own actions as you build,” I reminded them.
I didn’t think to add (particularly for that skeptical student and for those three adults in the back) that pattern recognition is one of those core mathematical thinking skills all students are expected to attain. The excitement of seeing students jump in and build with focus and determination distracted me. My fears started to evaporate.
There are lots of ways to build the pattern above, but let me show you one student’s straightforward method. Here’s how the first and second stages looked as she worked:
Figure 2
And here’s how the third stage developed:
Figure 3
Next, students shared their process, first with a partner, then with the whole group. For example, the student who built in the way shown above said,
I built the first stage first. That was one block. Then, for stage two, I added one upper block, one lower block, and then the blocks on the sides. Last, the one block on top. For the next stage I did the same thing . . . one upper block, one lower block, and then the blocks on the sides. Last, the block on top.
This student’s description showed she was noticing her pattern. As more students shared, it was clear all were exploring pattern. In this student’s case, her pattern was upper, lower, sides, top . . . upper, lower, sides, top . . .
Once more, the ninth graders split off into partnerships and worked to figure out a generalization of their actions and then record that generalization in an algebraic expression. In other words, their task was to use numbers and variables to show the repetition they noticed. This new expression would be a code, if you will, for how the pattern grows at any stage.
The variable n was used to specify the stage number. Here are some photos of the partners’ work on the white boards around the walls of the classroom:
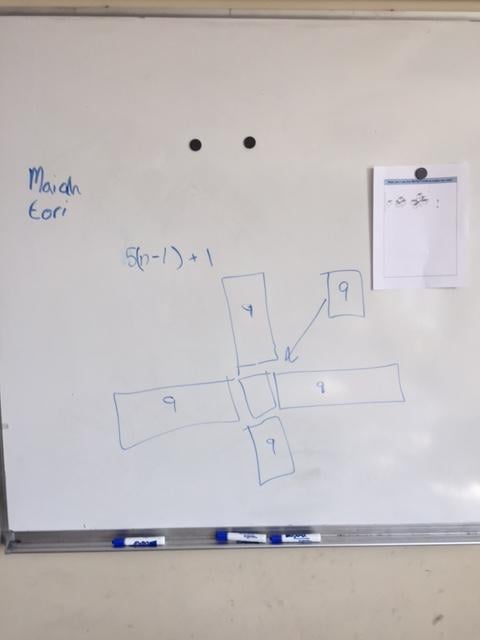
Figure 5
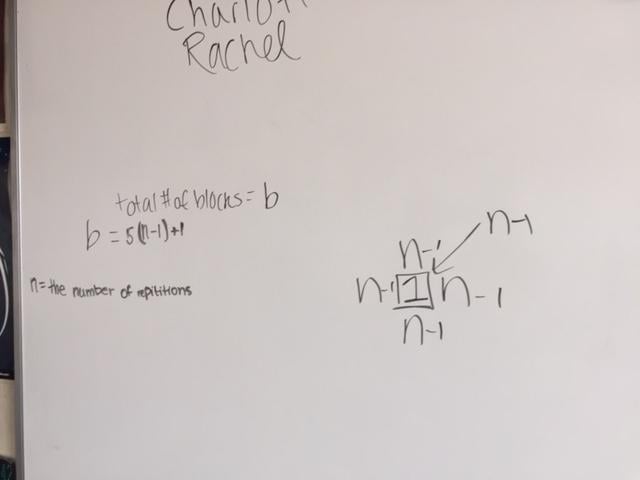
Figure 6
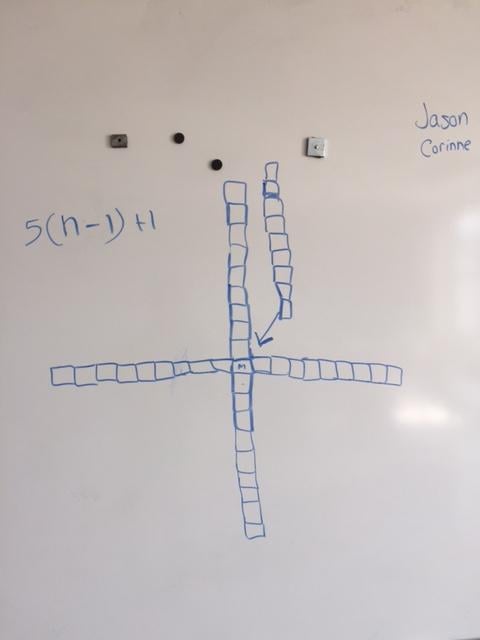
Figure 7
Just as I’d seen with younger students, the ninth graders described their insights to each other (and to me when I asked) using cubes to explain how they were working and what they were thinking. Only occasionally did they use their cubes to make the highest cube towers they possibly could! Which, of course, came crashing down on their desktops.
As I watched all of this I thought, High school math is definitely the place for me! I saw ninth graders using cubes to build (and to rebuild) structures as they deliberately noticed their actions. I believe these students needed this just as the younger learners did.
To be clear about the process of this whole task, the students had figured out that their repetition echoed the pattern itself. In other words, the stage they were building had five arms (four stretching out in an X-Y axis and the fifth arm towering straight up). These arms constitute the 5 in the equation 5(n - 1) + 1. And these five arms were always made with one less block than the stage number itself— thus the (n - 1).
And, then, there was the +1 for the additional lone block in the middle. Remember, stage 1 had just one block. That’s the +1.
Carry all this through to see the logic of the equation by substituting 1 for the n in (n - 1) and you get 5 multiplied by 0. The +1 is the one block that starts it all off. Stage one.
5(n - 1) + 1 can be read, “For any stage number n, build five arms (four stretching outward, one up) each having one less block than the stage number itself. Last, add a single block in the very middle. (Think back—upper, lower, sides, top . . .)
Voila!
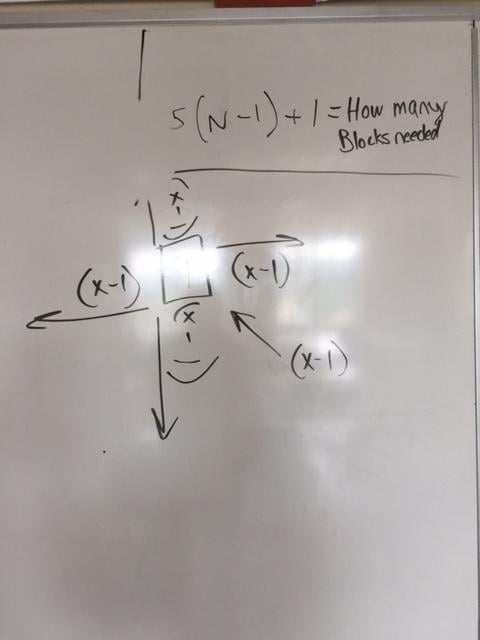
Figure 8
The use of visuals and manipulatives in math is often perceived as “babyish” and a sure sign of a student’s inability to do the work in a more sophisticated and acceptable way (in one’s head or on paper with lots of numbers). I don’t think I’m overstating things when I say it’s a common belief among teachers and students that math visuals and manipulatives are a crutch to be outgrown and an intervention to be used only when necessary.
On the contrary, these ninth graders have not outgrown the use of manipulatives to support and encourage their math thinking. I saw firsthand how these manipulatives were useful and, dare I say, even a pleasure to work with. Centimeter cubes through their visual and concrete nature allowed clearer access to the ideas we were exploring that day. Even at the high school honors level, visual tools are worth employing.
I’ve told you before that I was an English major. My entire teaching career up until the last few years has focused mainly on literacy instruction. And, although my leap to high school math ultimately failed, guess what the math bug has gotten me . . . I’m not teaching high school math (yet!) but I did recently move myself into a brand-new classroom for this school year. I’m teaching sixth-grade math at the middle school.
Math. That’s the place for me now.
Some examples of reflections from students at the high school
“Use of physical things . . . helps me notice repetition because . . . easy to visualize”
“Diagrams . . . helps me notice repetition because . . . I can have a visual to refer to”
“Images . . . helps me notice repetition because . . . I am a visual learner”
“Visual drawing . . . helps me notice repetition because . . . I can see what is changing”
Ian says it’s always productive to speak with students about “misfires and failures” and that they outweigh the learning moments of “triumphs.” He says we learn from how we tend to get things wrong. He is part of a year long collaboration with colleagues on the planning and teaching of writer’s workshop units of study. He is a 5th Grade (and former 1st Grade) Teacher, at New Franklin School. Boaler, Jo, and Lang. 2016 “Why Kids Should Use Their Fingers in Math Class.” The Atlantic. Atlantic Media Company, 13 April. Retrieved 8/16/2017 from https://www.theatlantic.com/education/archive/2016/04/why-kids-should-use-their-fingers-in-math-class/478053/
Kelemanik, Grace, Amy Lucenta, and Susan Janssen Creighton. 2016. Routines for Reasoning: Fostering the Mathematical Practices in All Students. Portsmouth, NH: Heinemann.
