One of my first moments of seeing the power of visuals in math learning came over a year ago, in June 2016. I was teaching fifth grade, and I gave my students an open-ended math task on a green sheet of grid paper with two different right triangles printed on it. I chose this task from several I’d gathered at a math conference that March.
This task held the promise of a different, and I hoped better, way to teach math. Until then I had been teaching each lesson pretty much as it was written in the curriculum guide, following along as best I could and finding myself unsatisfied and discouraged year after year.
Using that method, math was mostly about procedures prescribed to reach a foregone conclusion. Everyone in the room knew the answer was inside the pages of the book at my fingertips. What, then, was left for us to do? Perform for one another and demonstrate that we could (or, worse, couldn’t!) produce the correct answer? That’s all it felt like.
Done this way, there’s not much to engage anyone, teacher or student. There are few questions to ponder other than how to follow a procedure exactly, and even fewer opportunities to discover a place for oneself inside the work. In the way I’d always taught math, students and teacher were trapped outside. The mathematics stood apart, like a silver block of knowledge on a hilltop stubbornly waiting to see if we could crack its flawless surface.
To start the triangle task, students partnered up and went to different corners of the room. Zach, a distractible ball of energy, and Ella, a Hermione Granger protégé, got right to work.
Immediately, though, several partnerships around the room voiced protests: “Impossible,” one pair groaned. “How am I supposed to know?” another student grumbled.
Our class had studied rectangles, but we hadn’t really talked about how to find the area of triangles yet.
When the grumbles started, I thought to myself, “Is this too hard?” and began to think about an exit strategy.
Except, something stopped me. I waited a little longer and let the noise grow a little louder.
The words of my favorite presenter from that recent math conference replayed in my head: “Let kids grapple with big questions and struggle (to a degree) in search of their own solutions” (Margaret Smith, University of Pittsburgh).
So that’s what I did.
Despite the growing unrest, Zach and Ella had been uncharacteristically quiet with their heads down and their Crayola markers wiggling away over their sheet of grid paper. And, just as I decided to pull the plug on the task, Zach’s voice cut through the din.
“We got it!” he yelled.
The room fell quiet. Students turned their heads, and suspicious classmates drifted over to appraise Zach’s boast. Then, one after another, these envoys hurriedly returned to their own work.
Soon a new tone rippled through the classroom. Voices of “Oh!” and “Easy!” and “That’s all we have to do?” were heard.
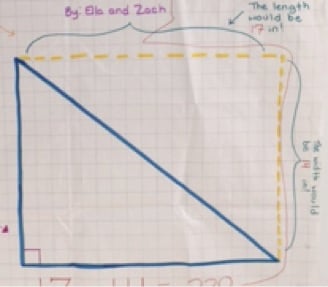
I walked over to Zach and Ella to take a look. True confession: I did not have a clear idea of what I was asking my class to do here. I had not seen this task done before. Yes, I was aware of the close similarities between the area of a right triangle (1/2 base * height) and the area of a rectangle (base * height), but when I saw Zach and Ella’s drawing, I was blown away. I was forced to acknowledge that I hadn’t really understood the relationship between the two shapes and their areas until that moment.
Zach and Ella’s drawing said it all:
In one fell swoop Zach and Ella cleared a path toward understanding by drawing that yellow dotted line to show the triangle as half of a rectangle. This made it possible to see the truth of their thinking and to deal with the problem in familiar terms—the area of a rectangle.
The now-clear relationship between the area of a right triangle and the area of a rectangle ignited understanding and excitement among the rest of the students.
In hindsight, I would have done many things differently in this lesson. But, as I thought over the richness of the work and how the conversation had sprung to life when Zach and Ella made that visual representation, it was clear to me that without that drawing, the whole thing would have just been talk.
This lesson began with the open-ended task, but it needed that other piece as well. It needed Zach and Ella’s drawing. I tried to imagine this lesson without their drawing and I couldn’t—it made the abstract concrete, and it gave the students the tools to move through their task and discover their own thinking.
Open-ended tasks. Giving kids room to explore and discover. Visual tools, in combination with numbers, providing the foundation for thinking and for conversations to take place . . .
These methods and ideas all sound good, and I’m pretty sure most of us have heard lots of teachers and big auditorium speakers say them many times before. But what really matters, and what really made the difference for me, was watching it happen in my own classroom with my own students. So, don’t take my word for it . . . real excitement awaits when you try it yourself.
Ian says it’s always productive to speak with students about “misfires and failures” and that they outweigh the learning moments of “triumphs.” He says we learn from how we tend to get things wrong. He is part of a yearlong collaboration with colleagues on the planning and teaching of writer’s workshop units of study. 5th Grade (and former 1st Grade) Teacher, at New Franklin School
