Math is much more than memorizing facts and following rules.
In Making Sense of Algebra, Paul Goldenberg, June Mark, and their colleagues look carefully at how our students think about mathematics. They explore five “Habits of Mind” that focus not just on the results of mathematical thinking, but on how proficient students do that thinking.
In today’s blog, which is the first of five adapted from the book, the authors talk about the habit of describing repeated reasoning.
Habits of Mind: Describing Repeated Reasoning
By Paul Goldenberg, June Mark, Jane Kang, Mary Fries, Cynthia Carter, and Tracy Cordner
Beginning with concrete examples and abstracting regularity from them is one nearly automatic approach mathematicians take to attack unfamiliar problems; it is a habit of the mathematical mind. The name that the Common Core invented for this element of mathematical practice is “Look for and express regularity in repeated reasoning.” Although students are still building this habit, they are—like novice drivers—not so natural and smooth, and they may need to be told to perform repeated experiments and describe their method.
The following exercise, at its simplest, is just a multiplication fact practice that might suit fourth or fifth grade, but it develops much more than fact memory and extends quickly to support algebraic goals. It is also a clear example of abstracting pattern from repeated reasoning. Students who know most but not all of the products of numbers less than or equal to 10, and who know how to use those to find simple products of multiples of 10, like 30 × 30, can enjoy this activity in which the teacher does not talk at all but produces a patterned calculation and invites students to join in.
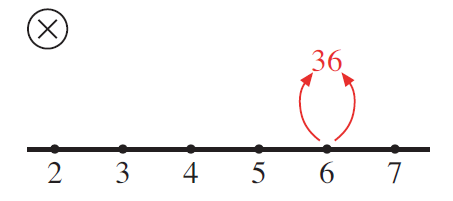
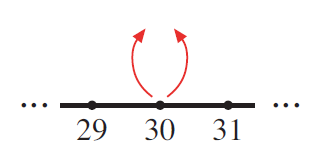
Sketch a segment of a number line, draw a pair of arrows upward from some number and, where the arrows meet, write that number times itself, like this. (Note: The circled X in each image is just one extra visual clue to keep multiplication in mind.)
Still with no words of explanation, draw another pair of arrows from the nearest neighbors of that number and write their product.
Start the same process at a new location.
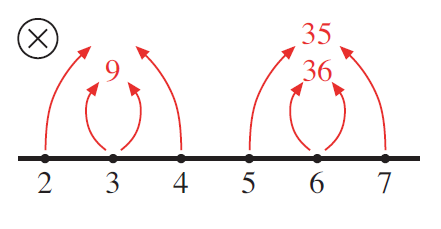
By now, most students see the pattern, so when you draw arrows up from that new number’s neighbors, you can turn to them and wait for them to say what to write.
Continue in the same way, now writing no numbers until they say what to write. After a while, the display might look like this.
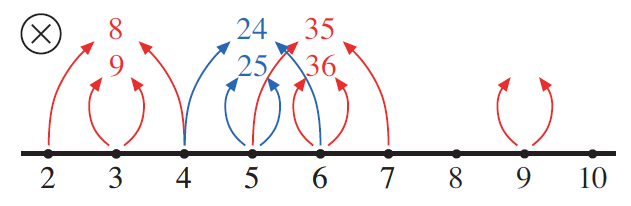
A few steps later, your display might look like this.
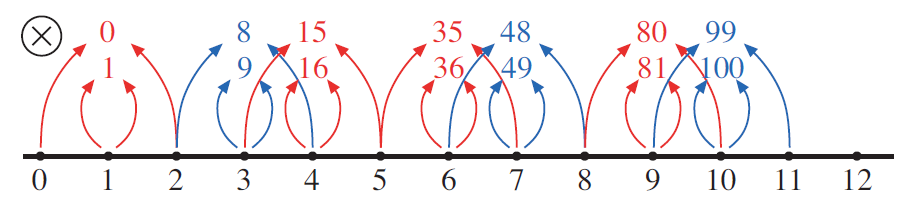
Still without you or your students saying anything about the pattern they’ve seen, draw a new segment of the number line and again invite students to call out the number.
When they do, continue as before, drawing arrows from the nearest neighbors.
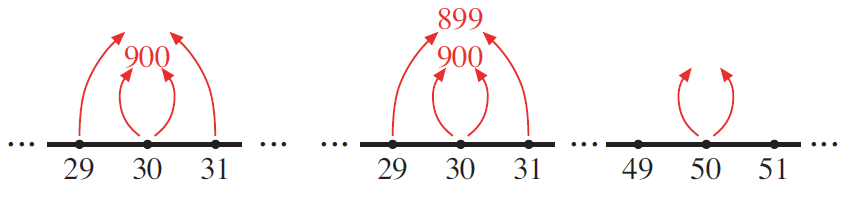
Everything up to this point has required only memory of known facts, but now, when they call out 899, they are using a pattern they abstracted from repeated reasoning. They have not, at this point, written the pattern in the language of algebra, or even expressed the pattern orally in their own native language, but they have enacted the pattern, shown that they see it and can use it. Click here for more detail on this type of exercise.
Consider another example:
Knowing how to add 9 (or 99) by thinking “add 10 (or 100) and subtract 1” can be a discovery rather than a “rule” a child is taught. There are obviously many ways of setting up experiences from which young children might make this discovery, but one way is to have children start with some number like 28 and respond as the teacher repeats, “10 more” (38), “10 more” (48), “10 more” (58), and so on. The learners may first need to count to find the next number—or even to verify that these rhyming answers really are the results of adding 10—but they soon hear the pattern in their responses because no other explanatory or instruction words are interfering. (This is a reason why it is important that the teacher say only the words ten more and not longer and more distracting talk like “Now add 10 to 38.”)
Children begin to express that discovery from repeated reasoning by saying the 68, 78, 88, almost without even the request for “10 more.” When the teacher later changes and asks for “nine more,” even young learners often see, on their own, that this is almost 10 more, and they make the correction spontaneously. Describing the discovery then becomes a case of expressing the regularity that was found through repeated reasoning. Young learners find it very exciting to add 99 the same way, first by repeating the experience of getting used to a simple computation, adding 100, and then by coming up with their own adjustment to add 99.
♦ ♦ ♦ ♦
Paul Goldenberg, June Mark, Jane Kang, Mary Fries, and Tracy Cordner work in the Learning and Teaching Division at Education Development Center (EDC), a non-profit organization that designs, implements, and evaluates programs to improve education, health, and economic opportunity worldwide. Cynthia Carter is a mathematics teacher at The Rashi School in Massachusetts.
