Tools should help students make sense of a mathematical world…and sense-making requires strategic thinking about which tools to use.
In Making Sense of Algebra, Paul Goldenberg, June Mark, and their colleagues look carefully at how our students think about mathematics. They explore five “Habits of Mind” that focus not just on the results of mathematical thinking, but on how proficient students do that thinking.
In today’s blog, which is the fourth of five adapted from the book, the authors talk about the habit of using tools strategically.
Habits of Mind: Using Tools Strategically
By Paul Goldenberg, June Mark, Jane Kang, Mary Fries, Cynthia Carter, and Tracy Cordner
Manipulatives, measurement instruments, calculators, and computers are all valuable tools. Paper and pencil is also a tool, valuable for much more than just calculation: competent use of that tool includes comfort with diagrams, tables, and graphs. Without diluting the meaning of “tool,” some broad mental models should also be thought of as tools—and, as the Common Core requires, students should acquire the disposition “to make sound decisions about when each of these tools might be helpful, recognizing both the insight to be gained and [the tools’] limitations.” Choosing when to pursue a calculation, look for an algorithm, or seek a contradiction is a clear example of choosing a tool strategically, a kind of thinking that, over time, becomes “second nature” for mathematicians: a habit of the mathematical mind.
All tools both aid and limit. Counters in grade 1 help develop skills and ideas connected with counting, but as a tool they strongly privilege positive integers. Though the Common Core sensibly puts the study of generalized fractions off until grade 3, even first graders come in knowing that they were 5, then 5 1/2, then 6, then 6 1/2, then 7, and counters don’t let them represent what they already know about those numbers—especially their order—in a helpful way. Rulers and tape measures are concrete versions of number lines. Sensibly selected, they provide a way to show where numbers like 5 1/2 live. They extend thinking to positive rational numbers. The number line diagram extends thinking to negative numbers. The number line, an array/area model for multiplication/division, and tables all complement the use of counters, and remain important and faithful images of mathematics through secondary and university education. Tools help us organize and perform experiments and extend our reach, our memory, or our precision, but they don’t do the problem. That remains our job.
The Common Core State Standards for Mathematical Practice call not just for using tools but for students to “make sound decisions about when each of these tools might be helpful.” Naturally, this requires that learners gain sufficient competence with the tools to recognize the differential power they offer. That may mean that from time to time, a particular tool is prescribed—or proscribed—until learners develop sufficient competency that they can make “sound decisions” about which tool to use.
But it also requires curriculum materials and teaching to include the kinds of problems that genuinely favor different tools and to give learners plenty of opportunities to decide for themselves which tool serves them best. For example, some computations are most sensibly done on a calculator, and some are most sensibly done in one’s head; if a curriculum does not regularly switch among these, students make a habit of pulling out the calculator automatically without thinking.
When one is using tools to model the mathematics, the choice of model matters. When children first learn multiplication in elementary school, it is often modeled with images like multiple equal-sized collections of pencils, or multiple plates with a fixed number of cookies each. For example, 3 plates of cookies 4 four cookies in each is 12 cookies: 3 × 4 = 12.
But with the “equal groups” model, it is nothing short of a miracle that 3 groups of 4 is the same as 4 groups of 3. This equal groups model illustrates one use of multiplication but hides a key property of the operation. A different image—the baking pan with the cookies laid out in an array—makes that entirely and intuitively apparent.
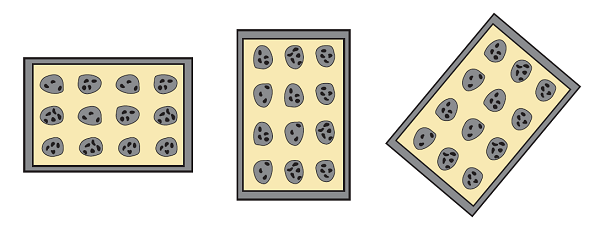
One can still use 3 + 3 + 3 + 3, if one wants, as a description of the picture, and 4 + 4 + 4 as a description of the same picture. Whether the multiplication expressions 3 × 4 and 4 × 3 are understood as “shorthand” for those addition expressions or as descriptions of rows and columns in the baking pan, it is clear that 3 × 4 = 4 × 3.
That same array model extends to allow 48 × 26 to be computed as (40 + 8) × (20 + 6).
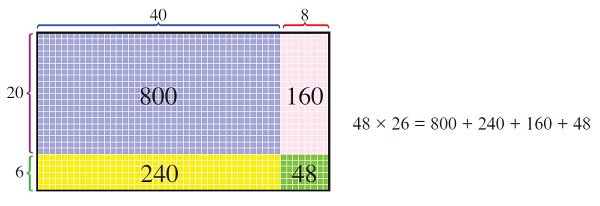
There is no need for the tiny details—we’re not counting anyway—so this becomes abstract.
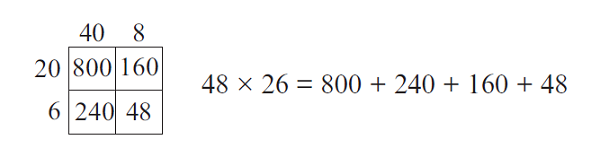
The cookies on a plate model serves only for small repeated addition. The array/area image models the standard multiplication algorithm and is generalizable: that is a practical tool.
♦ ♦ ♦ ♦
Paul Goldenberg, June Mark, Jane Kang, Mary Fries, and Tracy Cordner work in the Learning and Teaching Division at Education Development Center (EDC), a non-profit organization that designs, implements, and evaluates programs to improve education, health, and economic opportunity worldwide. Cynthia Carter is a mathematics teacher at The Rashi School in Massachusetts.
