Access a complete instructional sequence from But Why Does It Work? now.

♦ ♦ ♦ ♦

Mathematical argument—the ability of students to justify their thinking and engage with the reasoning of others—is not just for solving individual problems. Take the following question and discussion from a second grade class:

Craig and Luisa were playing a game with 52 pennies. Craig hid some of the pennies, and then there were 29 showing. How many did Craig hide?

Henry: I wanted to figure out how many pennies are left if you take away 29. So I subtracted 20 from 52, so that’s 32. Then I had to subtract 9 more, but it was easier to subtract ten and then add one back, so I got 22, then 22 + 1 = 23.

Melissa: I did it a different way. I said 29 + 1 is 30. Then you need 22 more to get to 52.

Teacher: Does anyone have questions about Henry’s or Melissa’s solutions?

Alberto: I don’t agree with Melissa. She said she got 22, but I got 23 like Henry.

Teacher: Melissa, do you understand Alberto’s thinking? Do you want to explain your solution?

Melissa: The answer isn’t 22. That was only how I got from 30 to 52. My answer is 23.

Henry: I don’t understand how you got your answer either. You were adding, and I think we should be subtracting.

Teacher: Melissa, explain a little more about how you figured out that 23 pennies were hidden. I noticed you had a picture with your work. It might help to use your picture to explain your thinking.

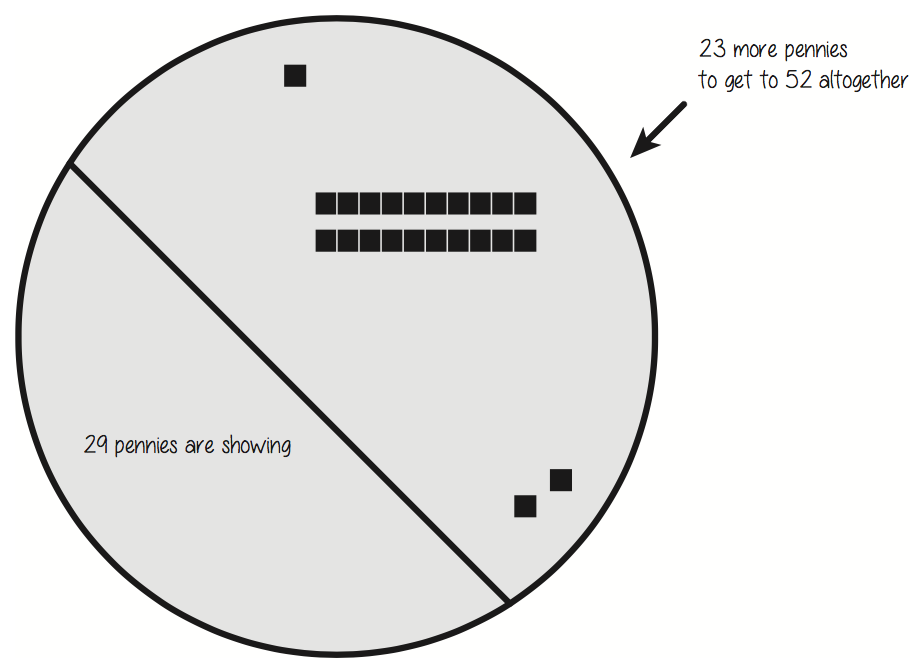
Melissa [showing her picture]: This whole circle is all 52 pennies. I didn’t draw all the pennies; it’s just like a pile of 52. So 29 of them are showing. That means I have to see how many pennies it takes to get up to 52, so first I added on 1—that’s this little square—now we’re up to 30. Then you add on 20, then you’re up to 50, that’s these two tens right here. Then you add on 2 more. So you had to add on 1, then 20, then 2, that’s 23 altogether that are hidden.

Henry and some other students: Oooh!

Henry: I get it. I started at 52 and took away the 29 part. Melissa started with the 29 and added up to figure out the part to get up to 52. It comes out the same.

Teacher: So how come Henry can solve this problem with subtraction and Melissa can solve it with addition? I’d like you to think more about this, and we’re going to come back to this question in our next session.

By the end of this discussion, the teacher is asking students to begin considering something more general about the behavior of the operations, something that applies to a whole class of problems. In this case, it is the relationship between addition and subtraction: Any problem that can be solved by subtraction can also be solved by finding a missing addend and vice versa.

As the students present their solution strategies, they are not only showing how they got an answer to the problem, but, with the guidance of their teacher, they are learning to engage in the practice of constructing mathematical arguments. As the class continues to discuss this idea, they will learn to articulate a conjecture about the relationship between subtracting and finding a missing addend and will use representations as the basis for their mathematical arguments about why it occurs.

But Why Does It Work? provides teachers with practical support for helping students justify their mathematical thinking and engage with the reasoning of their classmates. The book includes instructional sequences that offer a focused, structured, coherent approach to implementing work on mathematical argument into the elementary classroom.

Try a complete instructional sequence now ("Changing a Number in Addition or Subtraction") as part of a sample from But Why Does It Work?

♦ ♦ ♦ ♦

Susan Jo Russell is a Principal Scientist in the Education Research Collaborative at TERC.

Deborah Schifter is a Principal Research Scientist at the Education Development Center, Inc.

Reva Kasman is an Associate Professor of Mathematics at Salem State University.

Virginia Bastable is the Associate Director of the Mathematics Leadership Programs at Mount Holyoke College.

Traci Higgins is a Senior Researcher in the Education Research Collaborative at TERC.