I’d like to talk about algebra in a minute, but first, a quick quiz: What number do you see on each card?
I’d like to talk about algebra in a minute, but first, a quick quiz: What number do you see on each card?
If your brain works anything like mine, you saw the 9 on the purple card a lot faster than you counted the nine dots on the green card.
The dots represent nine as well, but they carry all sorts of other information: their shape, their differing sizes, the way they are scattered across the card. The numeral 9, on the other hand, gets straight to the point, the nine-ness, of nine. In fact, most adults are so accustomed to the symbol 9 that it feels like the most natural way to express the idea of nine.
This is one reason we use mathematical notation, because it strips away all the extraneous information and helps us communicate as directly as we can about mathematical ideas. We couldn’t live in a world where all quantities were represented with dots or hash marks. We need abstract representations of numbers.
And yet, imagine trying to teach a group of children the number system by starting with the numerals 1, 2, 3, and so on, without ever showing the kids a group of two blocks or three goldfish or any other concrete representations of quantity. It would seem like utter madness to ask students to commit all these symbols to memory without connecting them to other, more visually concrete representations of the numbers.
Certainly, our goal is for our students to feel comfortable with numerals, to the point that they see the 9 in the purple card faster than the nine on the green one. But our students need to see the connection between these two representations of a number so they can move fluidly between numerals, sets of dots, and other ways of representing numbers.
Aeriale Johnson, one of my fellow Fellows, is a kindergarten teacher, which means she spends a great deal of time helping her students grow comfortable with our number system. Aeriale’s classroom is brimming with different representations of number. Each of these representations draws her students’ attention to different aspects of our number system. The straws help students see how ones can be grouped and placed in the tens place, while the hundreds chart helps students see patterns in the rows and columns of the chart.
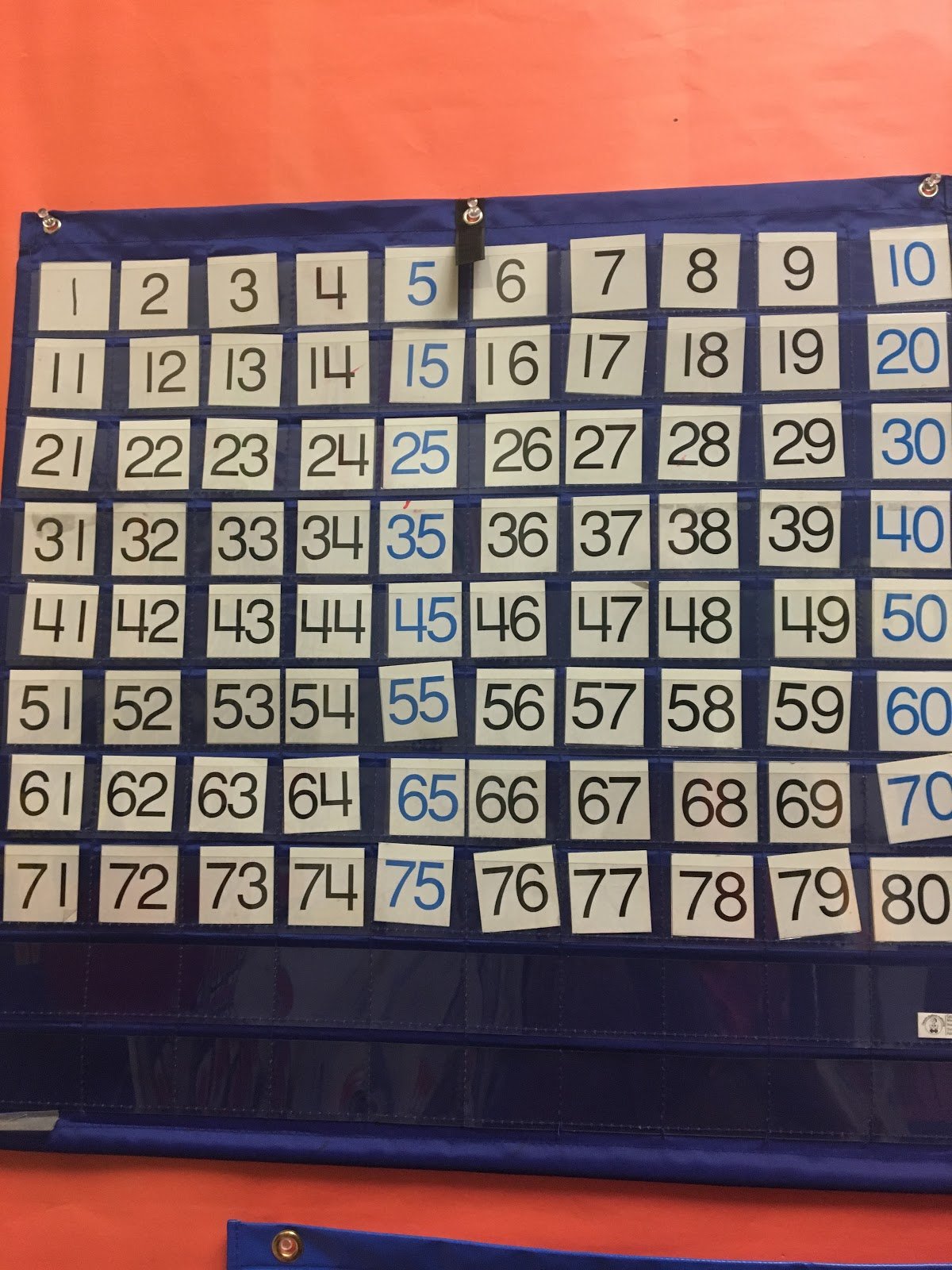
The good news is, Aeriale’s classroom is not the only kindergarten classroom where students explore multiple representations of number. In fact, many of these structures are adopted in schools throughout the country. This is why most students can not only interpret numerals fluently, but they can connect them to their underlying quantities and represent those quantities in all sorts of different ways.
I believe that middle school teachers need to explore and adopt a variety of representations of algebraic expressions so students build an understanding of what these symbols are meant to represent. As it stands, a typical middle school curriculum guides teachers to spend a great deal of time helping students to simplify algebraic expressions and solve algebraic equations, but precious little time helping students to interpret those expressions and equations, much less connect them to other representations of unknown quantities.
As I have continued my research, I have begun collecting representations of variables, some of which are shown below.
So, quick— - what is the value of x?
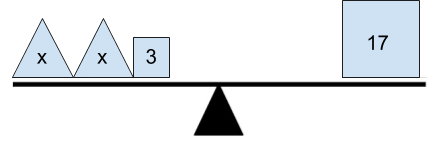
2x + 3 = 17
Each of these problems can be solved using the traditional procedure for solving equations: remove 3, then divide the remaining number by 2 to find the value of x.
But each of these representations offers different points of access for students as they build their understanding of algebraic equations. For instance, every problem contains two quantities, 2x + 3 and 17, that are equivalent. But that equivalence is represented in different ways. In the first image, the quantities balance when placed on a scale. In the tape diagram, the quantities create bars of equal lengths. In the number line, the quantities are at the same location on the number line. And in the equation, the equals sign indicates their equivalence.
Considering the number of students who enter middle school with an incomplete understanding of the equals sign, these other representations can help students internalize the idea of equivalence and how it can be represented.
To help our students connect these representations, we need activities that look quite different from typical equations tasks. Below is an example of a task I gave to my students at several points throughout our unit on expressions and equations. Upon first exposure, most of my students had no idea how to arrange the expressions on a number line, as shown in the first image. Although they were eighth graders who had been interacting with simple expressions such as 2x and x + 2 since sixth grade, they still couldn’t meaningfully connect those expressions to a quantity on the number line.
After they had a chance to debate and discuss these items in class, however, the students began to see how the visual structure of the number line could help them make sense of each expression. They saw the distance between 0 and 1 and realized that x + 1 would be just as far away from x. They started marking up the number lines, writing in numerical estimates for x, and plotting the other expressions based on those estimates.
As my students’ familiarity with this model grew, so did their ability to justify their choices. I had students debating the proper placement of - x and 2x + 1, which my students never did when we practiced tradition tasks with expressions. These conversations further strengthened the connections my students were making between the expressions and the visual model.
As they grew more confident with the model, I increased the complexity of the tasks. On this task from the following week, the same student from above was able to accurately place each expression on both number lines. Moreover, she was able to explain within her group why 2x is in the same location on both number lines below, while x + 2 and x - 1 are much closer to x in the second line. Since the scales of the number lines differ, the quantity of x represents a different number in each line, but 2x will always be twice as far from 0, regardless of the value of x. 
Although this task requires no simplifying or solving, it strengthens students’ abilities to look at an expression such as 2x and relate it to x, using the structure of a visual model.
We still should teach our students how to solve equations and combine like terms, certainly. But along the way, with the use of more visuals we’d give our students a chance to connect those algebraic moves with other representations, so that they could understand why and how the procedures work. Over time, our students would start to look at 2x + 3 and see the quantity that it represents, just as, in the opening paragraph, we see the number 9 and immediately grasp the quantity it represents.
When I began this research, I had hoped to find the perfect visual model to use when teaching expressions. As I tried different models in my classroom, however, I realized that using a variety of models was more important than choosing any single representation. The number line worked perfectly for some students, but others benefited more from the balance problems and the tape diagrams. There is no single representation that will unlock every student’s ability to read and interpret algebraic expressions, any more than there is a single representation that Aeriale uses to help her kindergartners grasp the concept of number. Instead, we must provide a wealth of opportunities for our students to connect expressions to different models so that each child finds the representation that best helps her interpret the meaning of an expression.
Kent Haines wants to change the way middle school students think about mathematics. He says he’d like students to solve equations more creatively and help them move “beyond memorized rules” in math practice. Kent teaches math at Simmons Middle School in Hoover, AL, and is a Heinemann Fellow in the 2016-2018 cohort. Follow him on Twitter @KentHaines
