The philosophy of Cognitively Guided Instruction (CGI) has helped hundreds of thousands of teachers learn more about children’s intuitive mathematical thinking and teach math more confidently. In today’s blog, which is adapted from Extending Children’s Mathematics: Fractions and Decimals, Susan Empson and Linda Levi look at the importance of helping students build an authentic understanding of fractions through solving and discussion word problems before introducing them to fractional symbols and notation.
by Susan Empson and Linda Levi
Four-year-old Emma had 7 cherries that she wanted to share with her aunt. She gave them out one by one to the two of them, saying to herself as she dealt, “1 for me, 1 for you. 1 for me, 1 for you. 1 for me, 1 for you. 1 for me.” Emma saw when she was done that she had 4 cherries and her aunt only had 3. Her aunt protested, and Emma slid a cherry from her share over to her aunt. Emma was surprised when she saw that the division was still unequal—now Emma had 3 and her aunt had 4! She picked up the extra cherry, gave it to herself again, and then giggled as she realized that no matter who she gave it to, the shares would not be equal. And then she had a wonderful idea: “Let’s cut it in 2!” Her aunt got a knife and cut the little cherry into 2 pieces. Satisfied with their equal shares, they ate their fruit.
Division into equal groups is a process that young children such as Emma understand intuitively. Building this foundation can begin as early as kindergarten, when children are capable of solving simple equal grouping problems much the way Emma did, by drawing on their intuitive understanding of sharing, measuring, grouping, and distribution. Consider this scenario:
In a first-grade classroom, the teacher gave her students this division problem:
4 children want to share 5 candy bars so that everyone gets the same amount. How much candy bar can each child have?
She encouraged the children to imagine themselves in this situation and to figure out the answer in a way that made sense to them. Almost all of the children drew pictures to help them think. Elliot decided to distribute 1 candy bar to each person, and then split the remaining candy bar into fourths, for a share of 1 and 1⁄4 candy bars each. Sofia decided to share each candy bar with all 4 children, for a share of 5⁄4 each. They showed how much each person would get by marking 1 person’s share. (Sofia also notated each person’s share as “5 qutrs,” for “five-quarters.”)
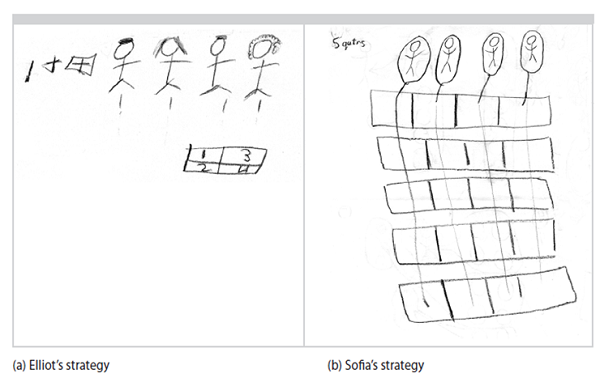
The division story problem involves fractions in its solution and can be solved by children without direct instruction. Elliot’s and Sofia’s informal knowledge of equal distribution and repeated halving helped them construct valid solutions; and they did not need to know how to use fraction symbols or terminology to solve these problems or report their solutions.
Solving and discussing Equal Sharing problems prepares children to learn from a variety of other problems involving fractions and decimals. Word problems help students connect their informal understanding of quantities and actions on quantities to new concepts of fractions and decimals. Equations help students make explicit their developing concepts of fractions and decimals and to become proficient in the use of number relationships and symbols.
Textbooks often start by introducing fraction symbols and then presenting a meaning for the symbol—usually, a part-whole or “n parts out of m equal parts” model.
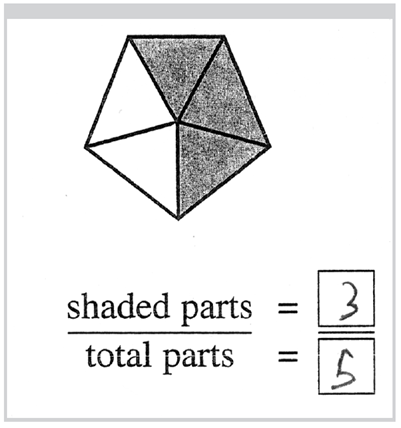
However, our research on how children’s thinking develops has led us to conclude that the opposite approach is more productive in the long run. Equal Sharing situations such as the one above are especially rich with mathematical meaning to which symbols can be later attached. The idea that meaning can precede symbols, or vice versa, is simplistic, but illustrates the contrast between different approaches to instruction.
Furthermore, fractions do not have a single meaning, such as n parts out of m parts. They can stand for amounts of stuff, such as 3⁄5 of a candy bar. They can stand for relationships between amounts, such as 3 candy bars for every 5 children, or processes involving amounts, such as 3 candy bars shared among 5 children. They can also of course be interpreted in terms of mathematical models, such as points on a number line or ordered pairs of numbers satisfying certain properties, as in the formal mathematical definition for rational numbers.
When children learn to think of fractions only, or mainly, as parts of wholes, it is hard for them to grasp what really makes a fraction what it is: a number whose value is determined by the multiplicative relationship between the numerator and the denominator. A common interpretation of this relationship involves how a part is related to the whole. But there are other, more powerful, interpretations. For example, here is what two sixth graders said when they were asked to explain what 2⁄3 meant.
Daisy: 2⁄3 is what you get if you take 2 things, split each into 3 equal pieces, and take 1 piece from each thing. Or you could take 2 pieces from 1 of the things. It doesn’t matter.
Roberto: 2⁄3 is like dividing 2 by 3. You can think of breaking 2 into 3 equal parts. Each part would be 2⁄3. Or you can think of how many threes fit into 2. You can’t get a whole 3 into 2 but you can get 2⁄3 of a 3 into 2.
Daisy and Roberto both understand 2⁄3 in terms of a multiplicative relationship between 2 and 3. (Because multiplication and division are inverse operations, we refer to reasoning that includes either as multiplicative.)
Thinking of fractions in these ways may seem beyond the grasp of elementary students, but it is not. The important thing is to begin by building meaning, and not by introducing the symbol alone. Because children’s experiences with slicing, splitting, distributing, measuring, and combining quantities are meaningful to them, problems that are based on these experiences are a rich source of meaning for fractions.
♦ ♦ ♦ ♦
Susan Empson is Professor of Curriculum and Instruction at the University of Texas–Austin.
Linda Levi is Director of Professional Development in Cognitively Guided Instruction for Teachers Development Group, a nonprofit organization dedicated to increasing all students' understanding and achievement through teacher professional development.